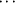 OW and N—O
OW and N—O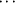 H—OW contacts between nitrite and water, and weak C—H
H—OW contacts between nitrite and water, and weak C—H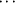 OW hydrogen bonds between pyridine and water. Thus, the intercalated water molecules act as bridges connecting the trans-[Ru(NO2)2(py)4] molecules into a three-dimensional network.
OW hydrogen bonds between pyridine and water. Thus, the intercalated water molecules act as bridges connecting the trans-[Ru(NO2)2(py)4] molecules into a three-dimensional network.Supporting information
Crystallographic Information File (CIF) https://doi.org/10.1107/S0108270111044672/mx3053sup1.cif | |
Structure factor file (CIF format) https://doi.org/10.1107/S0108270111044672/mx3053Isup2.hkl |
CCDC reference: 862217
trans-[Ru(NO2)2(py)4].2H2O powder was prepared as described previously (Schaniel et al., 2007, and references therein). The pale-yellow powder was dissolved in ethanol (2.10 τimes 10 -5 mol in 10 ml) and a few drops of water were added. Good yellow needle-like single crystals of (I) were obtained after slow evaporation over a period of a few days.
All H atoms were located in a difference Fourier synthesis, but those attached to C atoms were treated as riding on their parent C atoms, with C—H = 0.93 Å and Uiso(H) = 1.2Ueq(C). The H atoms of the water molecule were refined semi-freely by introducing a distance restraint of 0.84 (2) Å while constraining Uiso(H) to 1.5Ueq(O).
Data collection: CrysAlis CCD (Oxford Diffraction, 2008); cell refinement: CrysAlis RED (Oxford Diffraction, 2008); data reduction: CrysAlis RED (Oxford Diffraction, 2008); program(s) used to solve structure: SIR97 (Altomare et al., 1999); program(s) used to refine structure: SHELXL97 (Sheldrick, 2008); molecular graphics: Mercury (Macrae et al., 2008); software used to prepare material for publication: WinGX (Farrugia, 1999).
| [Ru(NO2)2(C5H5N)4]·2H2O | Dx = 1.630 Mg m−3 |
| Mr = 545.52 | Mo Kα radiation, λ = 0.71073 Å |
| Tetragonal, I41/acd | Cell parameters from 3452 reflections |
| Hall symbol: -I 4bd 2c | θ = 2.0–27.1° |
| a = 16.3418 (2) Å | µ = 0.76 mm−1 |
| c = 16.6448 (2) Å | T = 120 K |
| V = 4445.07 (9) Å3 | Prism, yellow |
| Z = 8 | 0.21 × 0.11 × 0.09 mm |
| F(000) = 2224 |
| Oxford Xcalibur diffractometer with Sapphire 3 CCD area detector | 1221 independent reflections |
| Radiation source: fine-focus sealed tube | 907 reflections with I > 2σ(I) |
| Graphite monochromator | Rint = 0.030 |
| Detector resolution: 19.64 pixels mm-1 | θmax = 27.0°, θmin = 3.0° |
| ω scans | h = −20→20 |
| Absorption correction: analytical (PLATON; Spek, 2009) | k = −20→20 |
| Tmin = 0.886, Tmax = 0.941 | l = −20→21 |
| 17299 measured reflections |
| Refinement on F2 | Primary atom site location: structure-invariant direct methods |
| Least-squares matrix: full | Secondary atom site location: difference Fourier map |
| R[F2 > 2σ(F2)] = 0.018 | Hydrogen site location: inferred from neighbouring sites |
| wR(F2) = 0.049 | H atoms treated by a mixture of independent and constrained refinement |
| S = 1.01 | w = 1/[σ2(Fo2) + (0.0301P)2] where P = (Fo2 + 2Fc2)/3 |
| 1221 reflections | (Δ/σ)max < 0.001 |
| 80 parameters | Δρmax = 0.26 e Å−3 |
| 1 restraint | Δρmin = −0.39 e Å−3 |
| [Ru(NO2)2(C5H5N)4]·2H2O | Z = 8 |
| Mr = 545.52 | Mo Kα radiation |
| Tetragonal, I41/acd | µ = 0.76 mm−1 |
| a = 16.3418 (2) Å | T = 120 K |
| c = 16.6448 (2) Å | 0.21 × 0.11 × 0.09 mm |
| V = 4445.07 (9) Å3 |
| Oxford Xcalibur diffractometer with Sapphire 3 CCD area detector | 1221 independent reflections |
| Absorption correction: analytical (PLATON; Spek, 2009) | 907 reflections with I > 2σ(I) |
| Tmin = 0.886, Tmax = 0.941 | Rint = 0.030 |
| 17299 measured reflections |
| R[F2 > 2σ(F2)] = 0.018 | 1 restraint |
| wR(F2) = 0.049 | H atoms treated by a mixture of independent and constrained refinement |
| S = 1.01 | Δρmax = 0.26 e Å−3 |
| 1221 reflections | Δρmin = −0.39 e Å−3 |
| 80 parameters |
Geometry. All e.s.d.'s (except the e.s.d. in the dihedral angle between two l.s. planes) are estimated using the full covariance matrix. The cell e.s.d.'s are taken into account individually in the estimation of e.s.d.'s in distances, angles and torsion angles; correlations between e.s.d.'s in cell parameters are only used when they are defined by crystal symmetry. An approximate (isotropic) treatment of cell e.s.d.'s is used for estimating e.s.d.'s involving l.s. planes. |
Refinement. Refinement of F2 against ALL reflections. The weighted R-factor wR and goodness of fit S are based on F2, conventional R-factors R are based on F, with F set to zero for negative F2. The threshold expression of F2 > σ(F2) is used only for calculating R-factors(gt) etc. and is not relevant to the choice of reflections for refinement. R-factors based on F2 are statistically about twice as large as those based on F, and R-factors based on ALL data will be even larger. |
| x | y | z | Uiso*/Ueq | ||
| O2 | 0.16048 (10) | 0.0000 | 0.2500 | 0.0329 (4) | |
| H2A | 0.1273 (10) | 0.0223 (11) | 0.2141 (11) | 0.049* | |
| Ru1 | 0.0000 | 0.2500 | 0.1250 | 0.01115 (9) | |
| N1 | −0.05987 (7) | 0.18279 (7) | 0.21495 (7) | 0.0143 (3) | |
| N2 | 0.08869 (7) | 0.16131 (7) | 0.1250 | 0.0170 (4) | |
| O1 | 0.07118 (7) | 0.08656 (6) | 0.13059 (6) | 0.0244 (3) | |
| C1 | −0.14074 (9) | 0.16593 (9) | 0.21282 (9) | 0.0180 (3) | |
| H1 | −0.1728 | 0.1890 | 0.1709 | 0.022* | |
| C2 | −0.17878 (10) | 0.11683 (10) | 0.26858 (9) | 0.0229 (4) | |
| H2 | −0.2359 | 0.1067 | 0.2650 | 0.028* | |
| C3 | −0.13324 (11) | 0.08240 (10) | 0.32987 (9) | 0.0257 (4) | |
| H3 | −0.1582 | 0.0479 | 0.3688 | 0.031* | |
| C4 | −0.05066 (10) | 0.09936 (9) | 0.33311 (9) | 0.0226 (4) | |
| H4 | −0.0176 | 0.0767 | 0.3745 | 0.027* | |
| C5 | −0.01667 (9) | 0.14948 (9) | 0.27567 (9) | 0.0184 (3) | |
| H5 | 0.0402 | 0.1612 | 0.2790 | 0.022* |
| U11 | U22 | U33 | U12 | U13 | U23 | |
| O2 | 0.0242 (9) | 0.0358 (10) | 0.0386 (10) | 0.000 | 0.000 | 0.0094 (9) |
| Ru1 | 0.01104 (10) | 0.01104 (10) | 0.01136 (13) | −0.00021 (9) | 0.000 | 0.000 |
| N1 | 0.0151 (6) | 0.0143 (6) | 0.0133 (6) | −0.0009 (5) | 0.0009 (5) | −0.0018 (5) |
| N2 | 0.0181 (6) | 0.0181 (6) | 0.0147 (9) | 0.0014 (7) | −0.0013 (5) | −0.0013 (5) |
| O1 | 0.0280 (6) | 0.0137 (6) | 0.0314 (7) | 0.0039 (5) | −0.0034 (5) | 0.0007 (5) |
| C1 | 0.0168 (8) | 0.0189 (8) | 0.0184 (8) | −0.0010 (7) | 0.0006 (6) | −0.0033 (7) |
| C2 | 0.0209 (8) | 0.0249 (9) | 0.0231 (9) | −0.0074 (7) | 0.0048 (7) | −0.0048 (7) |
| C3 | 0.0362 (10) | 0.0221 (9) | 0.0187 (9) | −0.0079 (7) | 0.0074 (8) | 0.0018 (7) |
| C4 | 0.0302 (9) | 0.0220 (8) | 0.0154 (8) | −0.0002 (7) | −0.0014 (7) | 0.0031 (7) |
| C5 | 0.0197 (8) | 0.0185 (8) | 0.0171 (8) | −0.0001 (6) | −0.0021 (6) | −0.0007 (7) |
| O2—H2A | 0.885 (14) | N2—O1 | 1.2582 (13) |
| Ru1—N2 | 2.0496 (17) | C1—C2 | 1.375 (2) |
| Ru1—N2i | 2.0496 (17) | C1—H1 | 0.9500 |
| Ru1—N1ii | 2.0989 (12) | C2—C3 | 1.382 (2) |
| Ru1—N1i | 2.0989 (12) | C2—H2 | 0.9500 |
| Ru1—N1iii | 2.0989 (12) | C3—C4 | 1.379 (2) |
| Ru1—N1 | 2.0989 (12) | C3—H3 | 0.9500 |
| N1—C5 | 1.3476 (18) | C4—C5 | 1.376 (2) |
| N1—C1 | 1.3503 (18) | C4—H4 | 0.9500 |
| N2—O1iii | 1.2582 (13) | C5—H5 | 0.9500 |
| N2—Ru1—N2i | 180.0 | O1iii—N2—O1 | 116.56 (17) |
| N2—Ru1—N1ii | 92.31 (3) | O1iii—N2—Ru1 | 121.72 (9) |
| N2i—Ru1—N1ii | 87.69 (3) | O1—N2—Ru1 | 121.72 (9) |
| N2—Ru1—N1i | 92.31 (3) | N1—C1—C2 | 122.92 (14) |
| N2i—Ru1—N1i | 87.68 (3) | N1—C1—H1 | 118.5 |
| N1ii—Ru1—N1i | 175.37 (6) | C2—C1—H1 | 118.5 |
| N2—Ru1—N1iii | 87.69 (3) | C1—C2—C3 | 119.48 (15) |
| N2i—Ru1—N1iii | 92.31 (3) | C1—C2—H2 | 120.3 |
| N1ii—Ru1—N1iii | 88.99 (6) | C3—C2—H2 | 120.3 |
| N1i—Ru1—N1iii | 91.20 (6) | C4—C3—C2 | 118.29 (15) |
| N2—Ru1—N1 | 87.68 (3) | C4—C3—H3 | 120.9 |
| N2i—Ru1—N1 | 92.32 (3) | C2—C3—H3 | 120.9 |
| N1ii—Ru1—N1 | 91.20 (6) | C5—C4—C3 | 119.18 (15) |
| N1i—Ru1—N1 | 88.99 (6) | C5—C4—H4 | 120.4 |
| N1iii—Ru1—N1 | 175.37 (6) | C3—C4—H4 | 120.4 |
| C5—N1—C1 | 116.75 (13) | N1—C5—C4 | 123.36 (14) |
| C5—N1—Ru1 | 120.14 (10) | N1—C5—H5 | 118.3 |
| C1—N1—Ru1 | 122.97 (10) | C4—C5—H5 | 118.3 |
| N2—Ru1—N1—C5 | 42.63 (10) | N1ii—Ru1—N2—O1 | −50.54 (6) |
| N2i—Ru1—N1—C5 | −137.37 (10) | N1i—Ru1—N2—O1 | 129.46 (6) |
| N1ii—Ru1—N1—C5 | 134.90 (12) | N1iii—Ru1—N2—O1 | −139.43 (6) |
| N1i—Ru1—N1—C5 | −49.72 (10) | N1—Ru1—N2—O1 | 40.57 (6) |
| N2—Ru1—N1—C1 | −132.82 (11) | C5—N1—C1—C2 | −0.6 (2) |
| N2i—Ru1—N1—C1 | 47.18 (11) | Ru1—N1—C1—C2 | 175.03 (11) |
| N1ii—Ru1—N1—C1 | −40.55 (10) | N1—C1—C2—C3 | −0.2 (2) |
| N1i—Ru1—N1—C1 | 134.82 (13) | C1—C2—C3—C4 | 0.5 (2) |
| N1ii—Ru1—N2—O1iii | 129.46 (6) | C2—C3—C4—C5 | −0.1 (2) |
| N1i—Ru1—N2—O1iii | −50.54 (6) | C1—N1—C5—C4 | 1.1 (2) |
| N1iii—Ru1—N2—O1iii | 40.56 (6) | Ru1—N1—C5—C4 | −174.67 (12) |
| N1—Ru1—N2—O1iii | −139.43 (6) | C3—C4—C5—N1 | −0.8 (2) |
| Symmetry codes: (i) −x, −y+1/2, z; (ii) y−1/4, x+1/4, −z+1/4; (iii) −y+1/4, −x+1/4, −z+1/4. |
Experimental details
| Crystal data | |
| Chemical formula | [Ru(NO2)2(C5H5N)4]·2H2O |
| Mr | 545.52 |
| Crystal system, space group | Tetragonal, I41/acd |
| Temperature (K) | 120 |
| a, c (Å) | 16.3418 (2), 16.6448 (2) |
| V (Å3) | 4445.07 (9) |
| Z | 8 |
| Radiation type | Mo Kα |
| µ (mm−1) | 0.76 |
| Crystal size (mm) | 0.21 × 0.11 × 0.09 |
| Data collection | |
| Diffractometer | Oxford Xcalibur diffractometer with Sapphire 3 CCD area detector |
| Absorption correction | Analytical (PLATON; Spek, 2009) |
| Tmin, Tmax | 0.886, 0.941 |
| No. of measured, independent and observed [I > 2σ(I)] reflections | 17299, 1221, 907 |
| Rint | 0.030 |
| (sin θ/λ)max (Å−1) | 0.639 |
| Refinement | |
| R[F2 > 2σ(F2)], wR(F2), S | 0.018, 0.049, 1.01 |
| No. of reflections | 1221 |
| No. of parameters | 80 |
| No. of restraints | 1 |
| H-atom treatment | H atoms treated by a mixture of independent and constrained refinement |
| Δρmax, Δρmin (e Å−3) | 0.26, −0.39 |
Computer programs: CrysAlis CCD (Oxford Diffraction, 2008), CrysAlis RED (Oxford Diffraction, 2008), SIR97 (Altomare et al., 1999), SHELXL97 (Sheldrick, 2008), Mercury (Macrae et al., 2008), WinGX (Farrugia, 1999).
| Bond length/angle | Experimental (this work) | Calculateda | Experimental (powder data)a |
| Ru1—N1(pyridine) | 2.0989 (12) | 2.12/2.13 | 2.07 (2)/2.13 (2)/2.00 (2)/2.08 (2) |
| Ru1—N2(nitro) | 2.0496 (17) | 2.10 | 2.23 (2)/2.22 (2) |
| N2—O1 | 1.2582 (13) | 1.27 | 1.12 (4)/1.18 (4)/1.14 (4)/1.15 (3) |
| O1—N2—O1i | 116.56 (17) | 117.8 | 122 (3)/135 (3) |
| N2—Ru1—N2ii | 180 | 179.9 | 175.2 (10) |
| N1—Ru1—N1i | 175.37 (6) | 179.4 | 177.0 (9)/177.8 (9) |
| Ru1—N2—O1 | 121.72 (9) | 120.8/121.3 | 111 (2)/110 (2)/113 (2)/118 (2) |
| Reference: (a) Schaniel et al. (2010). Symmetry codes: (i) -y+1/4, -x+1/4, -z+1/4; (ii) -x, -y+1/2, z. |
| The van der Waals radii sums are: O···O = 3.04 Å and O···H = 2.72 Å (Bondi, 1964). |
| Intermolecular distance | Angle | |
| Between a nitro group and water | ||
| N2—O1···O2 | 2.8427 (13) | 114.72 (7) |
| O2—H2A···O1 | 1.969 (18) | 168.9 (16) |
| Between pyridine and water | ||
| C2—H2···O2iii | 2.44 | 144 |
| Symmetry codes: (iii) x-1/2, y, -x+1/2. |

 journal menu
journal menu






![[Figure 1]](http://journals.iucr.org/c/issues/2011/12/00/mx3053/mx3053fig1thm.gif)
![[Figure 2]](http://journals.iucr.org/c/issues/2011/12/00/mx3053/mx3053fig2thm.gif)




Nitrosyl complexes have attracted a great interest over the past ten years because they present a reversible linkage isomerization under light irradiation between M—N—O and M—O—N forms, where M is a metallic atom (Fe, Co, Ru, Ni etc.) (Coppens et al., 2002, and references therein). The prototype compound is Na2[Fe(CN)5NO].2H2O (Hauser et al., 1977). Another kind of reversible photochemical transformation is reported between N-nitrite (M—NO2) and O-nitrite (M—ONO) molecules. The N-nitrite form of the molecule can usually be obtained during the synthesis of the corresponding nitrosyl complex M—N—O. The prototype compound of N-nitrite to O-nitrite linkage isomerization is [Co(NO2)(NH3)5]Cl2 (Grenthe & Nordin, 1979). Detailed crystallographic studies of these two kinds of materials are, however, still limited because of both difficulties in obtaining good single crystals and partial photochemical transformations (Coppens et al., 2002). A notable exception now exists in the family of nitrosyl complexes: trans-[RuCl(py)4(NO)](PF6)2.0.5H2O recently became a model system for the structural analysis of the two isomeric configurations of the NO ligand (Cormary et al., 2009), since the phototransformation from linear Ru—N—O (the so-called GS state) to linear Ru—O—N (the so-called MS1 state) is complete or quasi-complete in the single-crystal structure of the complex.
We report here the crystal structure of the N-nitrite form of trans-[Ru(NO2)2(py)4].2H2O, (I), which is an intermediate product obtained during the synthesis of trans-[RuCl(py)4(NO)](PF6)2.0.5H2O (Schaniel et al., 2007). High-quality yellow single crystals of (I) were obtained and the tetragonal space group I41/acd (Z = 8) was determined. This crystal structure differs from the powder structure previously determined in the orthorhombic space group Pna21, Z = 4 (Schaniel et al., 2010). In that work, the trans-[Ru(NO2)2(py)4] molecular geometry showed discrepancies with parameters derived from density functional theory (DFT) (Delley, 2006), which was discussed alongside the powder structure. Analysis of the single-crystal data reported here leads to a geometry for trans-[Ru(NO2)2(py)4] that is in good agreement with the DFT calculations performed for the free molecule. In addition, the single-crystal data enable discussion of the intermolecular interactions between trans-[Ru(NO2)2(py)4] and intercalated water.
The molecular geometry of trans-[Ru(NO2)2(py)4] differs significantly from that previously determined from powder data. The Ru atom lies at the intersection of three twofold axis (8b Wyckoff position) and is coordinated by four N atoms (labeled N1) of the pyridine rings as well as by two N atoms (labeled N2) of N-nitrite groups. The last two N atoms are located on a twofold screw axis (16f Wyckoff position). Thus, there is only one symmetry-independent pyridine ring and consequently an unique value for Ru1—N1 bond length. The two O atoms of the N-nitrite group are symmetry-equivalent and there are unique values for both Ru1—N2 and N2—O1 bond lengths (Fig. 1 and Table 1). Differences between the single-crystal structure and the previous powder structure are also clear from both bond lengths and angles values. In particular, the pyridine N—Ru distance (Ru1—N1) is longer than the nitrite N—Ru distance (Ru1—N2), while the powder structure led to the opposite conclusion (see Table 1). As mentioned above, DFT calculations are in agreement with the single-crystal structure (Table 1). Moreover, the Ru1—N2 bond length reported here [2.050 (2) Å] is not surprising when compared with values obtained from other nitro compounds of ruthenium, for example 2.033 (4) Å at 293 K in [Ru(tpy)(dpk)(NO2)]ClO4 (tpy is 2,2':6',2''-terpyridine? and dpk is ?; Sarkar et al., 2005), and 2.088 (1) and 2.091 (2) Å at 90 and 200 K, respectively, in [Ru(bpy)(NO)(NO2)](PF6)2 (bpy is ?,?'-bipyridine?; Kovalevsky et al., 2005). Another significant difference between the present single-crystal structure and the previous powder structure concerns the angular values involving the NO2 group. The Ru1—N2—O1 and O1—N2—O1i [symmetry code: (i) -y + 1/4, -x + 1/4, -z + 1/4] angles differ by between ca 5 and 18° (Table 1 and Fig. 1). In contrast, comparison between the trans-[Ru(NO2)2(py)4] molecular geometry determined here from single-crystal data (Table 1, column 1) and that calculated from DFT (Table 1, column 2) (Schaniel et al., 2010) again shows good agreement. Thus, the present single-crystal structure validates the DFT calculations.
Analysis of the intermolecular interactions in (I) shows that the solvent water molecules act as bridges connecting the trans-[Ru(NO2)2(py)4] complexes into a three-dimensional supramolecular network via (i) short O—H···O hydrogen bonds connecting the NO2 group and water, and (ii) weak C—H···O hydrogen bonds between pyridine rings and intercalated water (Table 2, and Figs. 1 and 2). Until now, the role of such close intermolecular contacts has not been discussed in the N-nitrite to O-nitrite photochemical process. One reason is that high-quality single-crystal data for such materials is largely missing and therefore DFT studies are usually limited to the intramolecular level (Schaniel et al., 2010). The single-crystal structure presented here could be used to undertake calculations beyond this level for a deeper understanding of the photochemical reaction. Indeed, IR spectroscopic investigations on powder samples (Schaniel et al., 2010) showed that, using light of wavelength 325 nm, about 50% of the trans-[Ru(NO2)2(py)4] molecules can be switched from the N-bound Ru—NO2 to the O-bound Ru-ONO configuration below T = 250 K. The reverse transformation is also observed with light in the wavelength range 405–442 nm. Further investigation of these photochemical reactions will be performed on the single crystals.