Periodic entanglement III: tangled degree-3 finite and layer net intergrowths from rare forests

Entanglements of two-dimensional honeycomb nets are constructed from free tilings of the hyperbolic plane (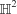) on triply periodic minimal surfaces. The 2-periodic nets that comprise the structures are guaranteed by considering regular, rare free tilings in 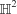. This paper catalogues an array of entanglements that are both beautiful and challenging for current classification techniques, including examples that are realized in metal–organic materials. The compactification of these structures to the genus-3 torus is considered as a preliminary method for generating entanglements of finite θ-graphs, potentially useful for gaining insight into the entanglement of the periodic structure. This work builds on previous structural enumerations given in Periodic entanglement Parts I and II [Evans et al. (2013). Acta Cryst. A69, 241–261; Evans et al. (2013). Acta Cryst. A69, 262–275].