Examples are given of recent abuses or debatable applications of the R-factor ratio test (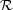 ) for the assignment of absolute configuration, and it is shown that some of the enhanced ratios that have been used do not necessarily imply a statistically significant reduction in α, the probability of making a wrong assignment. Reasons are given for believing α is usually seriously underestimated anyway, and that in marginal situations the weighted ratio,
) for the assignment of absolute configuration, and it is shown that some of the enhanced ratios that have been used do not necessarily imply a statistically significant reduction in α, the probability of making a wrong assignment. Reasons are given for believing α is usually seriously underestimated anyway, and that in marginal situations the weighted ratio, 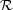 w, is a safer guide than
w, is a safer guide than 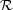 and can even contradict the assignment based on
and can even contradict the assignment based on 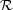 . Aids are given to facilitate the estimation of α that are much easier to use than interpolation or extrapolation from Hamilton's tables [Hamilton (1965). Acta Cryst. 18, 502-510]. The misconceptions led to a re-examination of the validity of Hamilton's application of linear-hypothesis testing to this particular problem. A more rigorous justification can be achieved by expressing the atomic scattering factors of all the anomalous scatterers in a crystal in the form f0j + f'j + iηf''j and refining η, the chirality/polarity parameter. Its standard deviation offers an alternative and more realistic index of the probability of an assignment. A postscript contributed by Professor G. M. Sheldrick reports very encouraging results for η refinement of three structures.
. Aids are given to facilitate the estimation of α that are much easier to use than interpolation or extrapolation from Hamilton's tables [Hamilton (1965). Acta Cryst. 18, 502-510]. The misconceptions led to a re-examination of the validity of Hamilton's application of linear-hypothesis testing to this particular problem. A more rigorous justification can be achieved by expressing the atomic scattering factors of all the anomalous scatterers in a crystal in the form f0j + f'j + iηf''j and refining η, the chirality/polarity parameter. Its standard deviation offers an alternative and more realistic index of the probability of an assignment. A postscript contributed by Professor G. M. Sheldrick reports very encouraging results for η refinement of three structures.

 journal menu
journal menu