In this article, a number of the results relevant to the concept of sublattices of a basic crystallographic lattice are reviewed, emphasizing particularly previously unpublished work on the algebraic aspects. A three-dimensional geometric lattice L can be considered as an infinite Abelian group under addition. A sublattice S of L, which is also three-dimensional, is a subgroup of L such that the finite quotient group,
is an Abelian group of order the index of S in L. The sublattice itself in its standard form is represented by an upper triangular matrix. The index of the sublattice is given by the determinant of this matrix. It is first noted that a sublattice described by an arbitrary basis set in L may be converted to this standard form. Next the sublattice is expressed as the intersection of a set of sublattices of individual index a power of a distinct prime, i.e.
where p1, p2 etc. are prime numbers and 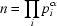 is the Euclidean factorization of n. This decomposition is important because it corresponds to the Sylow decomposition of the corresponding quotient group
It is also useful to be able to carry out two commutative binary operations on sublattices of L; these are to find their common sublattice of lowest index in L, which is their intersection
and their common superlattice of highest index in L, given by
where <> indicates the span of the sublattices.
is the Euclidean factorization of n. This decomposition is important because it corresponds to the Sylow decomposition of the corresponding quotient group
It is also useful to be able to carry out two commutative binary operations on sublattices of L; these are to find their common sublattice of lowest index in L, which is their intersection
and their common superlattice of highest index in L, given by
where <> indicates the span of the sublattices.

 journal menu
journal menu