research papers
Direct incorporation of experimental phase information in model refinement
aBiophysical Structural Chemistry, Leiden Institute of Chemistry, Gorlaeus Laboratories, Leiden University, PO Box 9502, 2300 RA Leiden, The Netherlands, and bStructural Biology Laboratory, Department of Chemistry, University of York, York YO10 5YW, England
*Correspondence e-mail: raj@chem.leidenuniv.nl
The incorporation of prior phase information into a formalism has been shown to strengthen model However, the currently available likelihood target using prior phase information has shortcomings; the `phased' target considers experimental phase information indirectly and statically in the form of Hendrickson–Lattman coefficients. Furthermore, the current target implicitly assumes that the prior phase information is independent of the calculated model This paper describes the derivation of a multivariate likelihood function that overcomes these shortcomings and directly incorporates experimental phase information from a single-wavelength anomalous diffraction (SAD) experiment. This function, which simultaneously refines heavy-atom and model parameters, has been implemented in the program REFMAC5. The SAD function used in conjunction with the automated model-building procedures of ARP/wARP leads to a successful solution when current likelihood functions fail in a test case shown.
Keywords: multivariate normal probability distribution; single-wavelength anomalous diffraction; automatic model building and refinement.
1. Introduction
A great deal of information is gained in experimentally phasing a molecule, yet the default procedure for automated model-building procedures combined with iterative structure (Perrakis et al., 1999![Perrakis, A., Morris, R. & Lamzin, V. S. (1999). Nature Struct. Biol. 6, 458-463. [Perrakis, A., Morris, R. & Lamzin, V. S. (1999). Nature Struct. Biol. 6, 458-463.]](../../../../../../logos/arrows/d_arr.gif) ; Terwilliger, 2003
; Terwilliger, 2003![Terwilliger, T. C. (2003). Acta Cryst. D59, 1174-1182. [Terwilliger, T. C. (2003). Acta Cryst. D59, 1174-1182.]](../../../../../../logos/arrows/d_arr.gif) ) only considers the diffraction data obtained from the native crystal and neglects any available experimental phase information.
) only considers the diffraction data obtained from the native crystal and neglects any available experimental phase information.
Previously, the incorporation of prior phase information has been shown to strengthen model (Pannu et al., 1998![Pannu, N. S., Murshudov, G. N., Dodson, E. J. & Read, R. J. (1998). Acta Cryst. D54, 1285-1294. [Pannu, N. S., Murshudov, G. N., Dodson, E. J. & Read, R. J. (1998). Acta Cryst. D54, 1285-1294.]](../../../../../../logos/arrows/d_arr.gif) ). However, the functional form of the likelihood target encodes the prior phase information statically in the form of Hendrickson–Lattman coefficients (Hendrickson & Lattman, 1970
). However, the functional form of the likelihood target encodes the prior phase information statically in the form of Hendrickson–Lattman coefficients (Hendrickson & Lattman, 1970![Hendrickson, W. A. & Lattman, E. E. (1970). Acta Cryst. B26, 136-143. [Hendrickson, W. A. & Lattman, E. E. (1970). Acta Cryst. B26, 136-143.]](../../../../../../logos/arrows/d_arr.gif) ). The likelihood function is then dependent on the reliability and accuracy of the phasing program used to generate the coefficients and does not allow the simultaneous of the associated heavy-atom and model parameters. Finally, the derivation of the current target incorporating prior phase information assumes that the prior phase distribution is independent of the model. This assumption is incorrect, as the phase information is used to build the model. All of the above shortcomings of the likelihood function utilizing prior phase information from Hendrickson–Lattman coefficients probably contributed to the reluctance to include prior information in automated model-building procedures.
). The likelihood function is then dependent on the reliability and accuracy of the phasing program used to generate the coefficients and does not allow the simultaneous of the associated heavy-atom and model parameters. Finally, the derivation of the current target incorporating prior phase information assumes that the prior phase distribution is independent of the model. This assumption is incorrect, as the phase information is used to build the model. All of the above shortcomings of the likelihood function utilizing prior phase information from Hendrickson–Lattman coefficients probably contributed to the reluctance to include prior information in automated model-building procedures.
To overcome these assumptions, a multivariate analysis directly modelling the correlations and errors in a phasing experiment and model should be applied; the resulting multivariate function would directly consider the diffraction data collected in the experiment. have played an important role in crystallography (e.g. see Bricogne, 2000![Bricogne, G. (2000). Advanced Special Functions and Applications: Proceedings of the Melfi School on Advanced Topics in Mathematics and Physics, edited by D. Cocolicchio, G. Dattoli & H. M. Srivastava, pp. 315-323. Rome: Aracne Editrice. [Bricogne, G. (2000). Advanced Special Functions and Applications: Proceedings of the Melfi School on Advanced Topics in Mathematics and Physics, edited by D. Cocolicchio, G. Dattoli & H. M. Srivastava, pp. 315-323. Rome: Aracne Editrice.]](../../../../../../logos/arrows/d_arr.gif) ) and joint probability distributions have recently led to promising results in detection (Burla et al., 2002
) and joint probability distributions have recently led to promising results in detection (Burla et al., 2002![Burla, M. C., Carrozzini, B., Cascarano, G. L., Giacovazzo, C., Polidori, G. & Siliqi, G. (2002). Acta Cryst. D58, 928-935. [Burla, M. C., Carrozzini, B., Cascarano, G. L., Giacovazzo, C., Polidori, G. & Siliqi, G. (2002). Acta Cryst. D58, 928-935.]](../../../../../../logos/arrows/d_arr.gif) ) and phasing (Giacovazzo & Siliqi, 2001a
) and phasing (Giacovazzo & Siliqi, 2001a![Giacovazzo, C. & Siliqi, G. (2001a). Acta Cryst. A57, 40-46. [Giacovazzo, C. & Siliqi, G. (2001a). Acta Cryst. A57, 40-46.]](../../../../../../logos/arrows/d_arr.gif) ,b
,b![Giacovazzo, C. & Siliqi, G. (2001b). Acta Cryst. A57, 414-419. [Giacovazzo, C. & Siliqi, G. (2001b). Acta Cryst. A57, 414-419.]](../../../../../../logos/arrows/d_arr.gif) , 2004
, 2004![Giacovazzo, C. & Siliqi, G. (2004). Acta Cryst. D60, 73-82. [Giacovazzo, C. & Siliqi, G. (2004). Acta Cryst. D60, 73-82.]](../../../../../../logos/arrows/d_arr.gif) ; Pannu et al., 2003
; Pannu et al., 2003![Pannu, N. S., McCoy, A. J. & Read, R. J. (2003). Acta Cryst. D59, 1801-1808. [Pannu, N. S., McCoy, A. J. & Read, R. J. (2003). Acta Cryst. D59, 1801-1808.]](../../../../../../logos/arrows/d_arr.gif) ; Pannu & Read, 2004
; Pannu & Read, 2004![Pannu, N. S. & Read, R. J. (2004). Acta Cryst. D60, 22-27. [Pannu, N. S. & Read, R. J. (2004). Acta Cryst. D60, 22-27.]](../../../../../../logos/arrows/d_arr.gif) ).
).
Below, we derive a multivariate single-wavelength anomalous diffraction (SAD) likelihood function that directly incorporates the measured Friedel pairs, ![[|F^+|]](teximages/ba5062fi1.gif) and
and ![[|F^-|]](teximages/ba5062fi2.gif) , and the associated calculated model structure factors into structure The function allows for the simultaneous of the heavy-atom and model parameters and thus directly and dynamically considers the experimental phase information from a SAD experiment.
, and the associated calculated model structure factors into structure The function allows for the simultaneous of the heavy-atom and model parameters and thus directly and dynamically considers the experimental phase information from a SAD experiment.
The SAD likelihood function has been implemented in the program REFMAC5 (Murshudov et al., 1997![Murshudov, G. N., Vagin, A. A. & Dodson, E. J. (1997). Acta Cryst. D53, 240-255. [Murshudov, G. N., Vagin, A. A. & Dodson, E. J. (1997). Acta Cryst. D53, 240-255.]](../../../../../../logos/arrows/d_arr.gif) ) from the CCP4 package (Collaborative Computational Project, Number 4, 1994
) from the CCP4 package (Collaborative Computational Project, Number 4, 1994![Collaborative Computational Project, Number 4 (1994). Acta Cryst. D50, 760-763. [Collaborative Computational Project, Number 4 (1994). Acta Cryst. D50, 760-763.]](../../../../../../logos/arrows/d_arr.gif) ). The newly implemented SAD function was compared with other targets and performs favourably. In a test case, the SAD function in conjunction with the automated model-building procedures implemented in ARP/wARP (Perrakis et al., 1999
). The newly implemented SAD function was compared with other targets and performs favourably. In a test case, the SAD function in conjunction with the automated model-building procedures implemented in ARP/wARP (Perrakis et al., 1999![Perrakis, A., Morris, R. & Lamzin, V. S. (1999). Nature Struct. Biol. 6, 458-463. [Perrakis, A., Morris, R. & Lamzin, V. S. (1999). Nature Struct. Biol. 6, 458-463.]](../../../../../../logos/arrows/d_arr.gif) ) leads to a correctly built model when current likelihood functions fail.
) leads to a correctly built model when current likelihood functions fail.
2. Implementation and test cases
An analysis of the complex multivariate distribution applied to many crystallographic experiments, including heavy-atom phasing by and model in the presence of multiple data sets and models, has been performed (Pannu et al., 2003![Pannu, N. S., McCoy, A. J. & Read, R. J. (2003). Acta Cryst. D59, 1801-1808. [Pannu, N. S., McCoy, A. J. & Read, R. J. (2003). Acta Cryst. D59, 1801-1808.]](../../../../../../logos/arrows/d_arr.gif) ). The distribution discussed in this paper can be applied to account explicitly for the correlations and errors in a SAD experiment when applied to both SAD phasing and model The multivariate conditional probability distribution for the of the two observed structure-factor amplitudes,
). The distribution discussed in this paper can be applied to account explicitly for the correlations and errors in a SAD experiment when applied to both SAD phasing and model The multivariate conditional probability distribution for the of the two observed structure-factor amplitudes, ![[|F^+|]](teximages/ba5062fi1.gif) and
and ![[|F^-|]](teximages/ba5062fi2.gif) , given the Friedel structure factors calculated from the model, Fc+ =
, given the Friedel structure factors calculated from the model, Fc+ = ![[|F_c^+| \exp(i \alpha_c^+)]](teximages/ba5062fi6.gif) and
and ![[(F_c^-)^\ast = |F_c^-| \exp(-i \alpha_c^-)]](teximages/ba5062fi7.gif) , is shown below,
, is shown below,
where
In the above equations, Σ4 is the (Hermitian) covariance matrix of the complex Gaussian distribution P(F+, F-, Fc+, Fc-), with the elements of its inverse denoted zjk = ajk + ibjk. Σ2 is the covariance matrix of the bivariate Gaussian distribution P(Fc+, Fc-), with real and imaginary components of its inverse denoted cij and dij. The covariance matrices Σ4 and Σ2 were calculated using the expressions derived by Pannu et al. (2003![Pannu, N. S., McCoy, A. J. & Read, R. J. (2003). Acta Cryst. D59, 1801-1808. [Pannu, N. S., McCoy, A. J. & Read, R. J. (2003). Acta Cryst. D59, 1801-1808.]](../../../../../../logos/arrows/d_arr.gif) ) and account for experimental errors and the correlation between structure factors.
) and account for experimental errors and the correlation between structure factors.
In Appendix A![[link]](../../../../../../logos/arrows/d_arr.gif) , the probability distribution of two observations given N models is derived. The SAD likelihood function shown above is a special case of this general distribution when there are only two models (i.e. N = 2). A likelihood function conditional on N models may be applied to multiple models output from an NMR experiment or from simulated-annealing optimization techniques (Rice & Brünger, 1994
, the probability distribution of two observations given N models is derived. The SAD likelihood function shown above is a special case of this general distribution when there are only two models (i.e. N = 2). A likelihood function conditional on N models may be applied to multiple models output from an NMR experiment or from simulated-annealing optimization techniques (Rice & Brünger, 1994![Rice, L. M. & Brünger, A. T. (1994). Proteins, 19, 277-290. [Rice, L. M. & Brünger, A. T. (1994). Proteins, 19, 277-290.]](../../../../../../logos/arrows/d_arr.gif) ) or when refining N related models obtained from conditional dynamics (Scheres & Gros, 2001
) or when refining N related models obtained from conditional dynamics (Scheres & Gros, 2001![Scheres, S. H. W. & Gros, P. (2001). Acta Cryst. D57, 1820-1828. [Scheres, S. H. W. & Gros, P. (2001). Acta Cryst. D57, 1820-1828.]](../../../../../../logos/arrows/d_arr.gif) ).
).
The `SAD' likelihood function discussed below is the sum over all reflections of the minus natural logarithm of the derived probability distribution (1)![[link]](../../../../../../logos/arrows/d_arr.gif) to obtain a function suitable for minimization. To ensure that the matrix remains positive definite, the inverse of the covariance matrix was calculated from the eigenvectors using only positive eigenvalues with LAPACK routines (Anderson et al., 1999
to obtain a function suitable for minimization. To ensure that the matrix remains positive definite, the inverse of the covariance matrix was calculated from the eigenvectors using only positive eigenvalues with LAPACK routines (Anderson et al., 1999![Anderson, E., Bai, Z., Bischof, C., Blackford, S., Demmel, J., Dongarra, J., Du Croz, J., Greenbaum, A., Hammarling, S., McKenney, A. & Sorensen, D. (1999). LAPACK Users' Guide, 3rd ed. Philadelphia: Society for Industrial and Applied Mathematics. [Anderson, E., Bai, Z., Bischof, C., Blackford, S., Demmel, J., Dongarra, J., Du Croz, J., Greenbaum, A., Hammarling, S., McKenney, A. & Sorensen, D. (1999). LAPACK Users' Guide, 3rd ed. Philadelphia: Society for Industrial and Applied Mathematics.]](../../../../../../logos/arrows/d_arr.gif) ).
).
The SAD function derived above was implemented in the program REFMAC5 (version 5.1.24; Murshudov et al., 1997![Murshudov, G. N., Vagin, A. A. & Dodson, E. J. (1997). Acta Cryst. D53, 240-255. [Murshudov, G. N., Vagin, A. A. & Dodson, E. J. (1997). Acta Cryst. D53, 240-255.]](../../../../../../logos/arrows/d_arr.gif) ) and compared with the `Rice' likelihood function lacking prior phase information (Bricogne & Irwin, 1996
) and compared with the `Rice' likelihood function lacking prior phase information (Bricogne & Irwin, 1996![Bricogne, G. & Irwin, J. (1996). Proceedings of the CCP4 Study Weekend. Macromolecular Refinement, edited by E. J. Dodson, M. Moore, A. Ralph & S. Bailey, pp. 85-92. Warrington: Daresbury Laboratory. [Bricogne, G. & Irwin, J. (1996). Proceedings of the CCP4 Study Weekend. Macromolecular Refinement, edited by E. J. Dodson, M. Moore, A. Ralph & S. Bailey, pp. 85-92. Warrington: Daresbury Laboratory.]](../../../../../../logos/arrows/d_arr.gif) ; Murshudov et al., 1997
; Murshudov et al., 1997![Murshudov, G. N., Vagin, A. A. & Dodson, E. J. (1997). Acta Cryst. D53, 240-255. [Murshudov, G. N., Vagin, A. A. & Dodson, E. J. (1997). Acta Cryst. D53, 240-255.]](../../../../../../logos/arrows/d_arr.gif) ; Pannu & Read, 1996
; Pannu & Read, 1996![Pannu, N. S. & Read, R. J. (1996). Acta Cryst. A52, 659-668. [Pannu, N. S. & Read, R. J. (1996). Acta Cryst. A52, 659-668.]](../../../../../../logos/arrows/d_arr.gif) ), denoted below as Rice, and the likelihood function encoding prior phase information with Hendrickson–Lattman coefficients (Pannu et al., 1998
), denoted below as Rice, and the likelihood function encoding prior phase information with Hendrickson–Lattman coefficients (Pannu et al., 1998![Pannu, N. S., Murshudov, G. N., Dodson, E. J. & Read, R. J. (1998). Acta Cryst. D54, 1285-1294. [Pannu, N. S., Murshudov, G. N., Dodson, E. J. & Read, R. J. (1998). Acta Cryst. D54, 1285-1294.]](../../../../../../logos/arrows/d_arr.gif) ), denoted below as MLHL.
), denoted below as MLHL.
For the two test cases described below, the automated model-building program ARP/wARP (version 6.0; Perrakis et al., 1999![Perrakis, A., Morris, R. & Lamzin, V. S. (1999). Nature Struct. Biol. 6, 458-463. [Perrakis, A., Morris, R. & Lamzin, V. S. (1999). Nature Struct. Biol. 6, 458-463.]](../../../../../../logos/arrows/d_arr.gif) ) employing the modified REFMAC5 program from the CCP4 suite (version 4.2.2; Collaborative Computational Project, Number 1994
) employing the modified REFMAC5 program from the CCP4 suite (version 4.2.2; Collaborative Computational Project, Number 1994![Collaborative Computational Project, Number 4 (1994). Acta Cryst. D50, 760-763. [Collaborative Computational Project, Number 4 (1994). Acta Cryst. D50, 760-763.]](../../../../../../logos/arrows/d_arr.gif) ) for iterative model was used. The sequence information for the protein was not supplied to ARP/wARP. Furthermore, the default parameters were used in the running of the program, unless otherwise stated below. In particular, the same low-resolution cutoff, obtained by viewing a Wilson plot as suggested by ARP/wARP, was used in both test cases for all target functions. We have also re-run the test cases using no low-resolution cutoff. While using the whole resolution range, there were no significant changes over the results presented below for the SAD function, while the MLHL function produced significantly poorer results in both test cases and the Rice function produced poorer results in the thioesterase test case.
) for iterative model was used. The sequence information for the protein was not supplied to ARP/wARP. Furthermore, the default parameters were used in the running of the program, unless otherwise stated below. In particular, the same low-resolution cutoff, obtained by viewing a Wilson plot as suggested by ARP/wARP, was used in both test cases for all target functions. We have also re-run the test cases using no low-resolution cutoff. While using the whole resolution range, there were no significant changes over the results presented below for the SAD function, while the MLHL function produced significantly poorer results in both test cases and the Rice function produced poorer results in the thioesterase test case.
For both test cases, the anomalous was determined, refined and phased automatically using the CRANK suite (Ness et al., 2004![Ness, S. R., de Graaff, R. A. G., Abrahams, J. P. & Pannu, N. S. (2004). Structure, 12, 1753-1761. [Ness, S. R., de Graaff, R. A. G., Abrahams, J. P. & Pannu, N. S. (2004). Structure, 12, 1753-1761.]](../../../../../../logos/arrows/d_arr.gif) ). CRANK used the programs CRUNCH2 (de Graaff et al., 2001
). CRANK used the programs CRUNCH2 (de Graaff et al., 2001![Graaff, R. A. G. de, Hilge, M., van der Plas, J. L. & Abrahams, J. P. (2001). Acta Cryst. D57, 1857-1862. [Graaff, R. A. G. de, Hilge, M., van der Plas, J. L. & Abrahams, J. P. (2001). Acta Cryst. D57, 1857-1862.]](../../../../../../logos/arrows/d_arr.gif) ) for detection, BP3 for and phasing (Pannu & Read, 2004
) for detection, BP3 for and phasing (Pannu & Read, 2004![Pannu, N. S. & Read, R. J. (2004). Acta Cryst. D60, 22-27. [Pannu, N. S. & Read, R. J. (2004). Acta Cryst. D60, 22-27.]](../../../../../../logos/arrows/d_arr.gif) ) and DM for density modification (Cowtan, 1994
) and DM for density modification (Cowtan, 1994![Cowtan, K. (1994). Jnt CCP4/ESF-EAMCB Newsl. Protein Crystallogr. 31, 34-38. [Cowtan, K. (1994). Jnt CCP4/ESF-EAMCB Newsl. Protein Crystallogr. 31, 34-38.]](../../../../../../logos/arrows/d_arr.gif) ). The Hendrickson–Lattmann coefficients required for the MLHL function were obtained from BP3. Furthermore, the refined anomalous from BP3 was input into ARP/wARP and REFMAC5 for all target functions in order to allow further For all likelihood functions and test cases, 250 cycles of automated model building with iterative structure were performed and the results of each likelihood function are compared with the final refined structure using the program SFTOOLS (Bart Hazes, unpublished work).
). The Hendrickson–Lattmann coefficients required for the MLHL function were obtained from BP3. Furthermore, the refined anomalous from BP3 was input into ARP/wARP and REFMAC5 for all target functions in order to allow further For all likelihood functions and test cases, 250 cycles of automated model building with iterative structure were performed and the results of each likelihood function are compared with the final refined structure using the program SFTOOLS (Bart Hazes, unpublished work).
2.1. Subtilisin test-data set
The first test case used was the protein subtilisin, which contains an anomalous signal from three calcium ions. The data were collected using synchrotron radiation at a wavelength of 1.54 Å. More information on this data set can be obtained from Dauter et al. (2002![Dauter, Z., Dauter, M. & Dodson, E. J. (2002). Acta Cryst. D58, 494-506. [Dauter, Z., Dauter, M. & Dodson, E. J. (2002). Acta Cryst. D58, 494-506.]](../../../../../../logos/arrows/d_arr.gif) ). The resolution range 1.77–8.2 Å was used for all likelihood functions and the starting map had a relatively high phase error of about 58°. The quality of the starting map and the performance of the three likelihood functions in the automated model-building test are shown in Table 1
). The resolution range 1.77–8.2 Å was used for all likelihood functions and the starting map had a relatively high phase error of about 58°. The quality of the starting map and the performance of the three likelihood functions in the automated model-building test are shown in Table 1![[link]](../../../../../../logos/arrows/d_arr.gif) .
.
| ||||||||||||||||||||||||||||||||
The results show that ARP/wARP in combination with the SAD function in REFMAC5 was able to build the vast majority of the model (256 of 275 residues), while the other targets failed. We were unable to improve the performance of the other target functions by changing any option in ARP/wARP or REFMAC5. The large difference in phase error and map correlation between the likelihood functions highlights the success of the SAD function. Fig. 1![[link]](../../../../../../logos/arrows/d_arr.gif) shows the models built by ARP/wARP using the SAD target (shown in red) superimposed on the final refined model (shown in blue).
shows the models built by ARP/wARP using the SAD target (shown in red) superimposed on the final refined model (shown in blue).
![[Figure 1]](ba5062fig1thm.gif) | Figure 1 Subtilisin models constructed by ARP/wARP using the SAD function (shown in red) superimposed on the final refined structure (shown in blue). |
Fig. 2![[link]](../../../../../../logos/arrows/d_arr.gif) shows the change in the phase error as a function of the automated model-building cycle for all three likelihood functions. The Rice function was unable to lower the phase error. The MLHL target shows a similar phase-error improvement as the SAD function in the first cycles, but does not build or improve the model in subsequent cycles. In contrast, the SAD function continues to improve the phases allowing ARP/wARP/REFMAC5 to build the model to near-completion.
shows the change in the phase error as a function of the automated model-building cycle for all three likelihood functions. The Rice function was unable to lower the phase error. The MLHL target shows a similar phase-error improvement as the SAD function in the first cycles, but does not build or improve the model in subsequent cycles. In contrast, the SAD function continues to improve the phases allowing ARP/wARP/REFMAC5 to build the model to near-completion.
![[Figure 2]](ba5062fig2thm.gif) | Figure 2 The dependence of phase error versus automated model-building cycle for all three likelihood functions in the subtilisin test case. The black curve shows the change in the phase error for the Rice function, the light grey curve is for MLHL and the dark grey curve is for the SAD function. |
2.2. Thioesterase test-data set
The second test case used is a selenomethionine thioesterase peak-wavelength data set collected at beamline X9B at Brookhaven National Laboratory with anomalous signal from the eight Se atoms (Li et al., 2000![Li, J., Derewenda, U., Dauter, Z., Smith, S. & Derewenda, Z. S. (2000). Nature Struct. Biol. 7, 555-559. [Li, J., Derewenda, U., Dauter, Z., Smith, S. & Derewenda, Z. S. (2000). Nature Struct. Biol. 7, 555-559.]](../../../../../../logos/arrows/d_arr.gif) ; Dauter et al., 2002
; Dauter et al., 2002![Dauter, Z., Dauter, M. & Dodson, E. J. (2002). Acta Cryst. D58, 494-506. [Dauter, Z., Dauter, M. & Dodson, E. J. (2002). Acta Cryst. D58, 494-506.]](../../../../../../logos/arrows/d_arr.gif) ). The resolution range 2.52–8.3 Å was used for all likelihood functions in the procedure and the starting map input into the automated model-building procedure had a relatively low phase error of about 42°. The results of this automated model-building test case for the three likelihood functions are shown in Table 2
). The resolution range 2.52–8.3 Å was used for all likelihood functions in the procedure and the starting map input into the automated model-building procedure had a relatively low phase error of about 42°. The results of this automated model-building test case for the three likelihood functions are shown in Table 2![[link]](../../../../../../logos/arrows/d_arr.gif) .
.
| ||||||||||||||||||||||||||||||||
Table 2![[link]](../../../../../../logos/arrows/d_arr.gif) shows that both likelihood functions incorporating prior phase information performed equally well and to the same phase error, while the likelihood function lacking prior phase information (i.e. the Rice function) performed significantly more poorly.
shows that both likelihood functions incorporating prior phase information performed equally well and to the same phase error, while the likelihood function lacking prior phase information (i.e. the Rice function) performed significantly more poorly.
3. Discussion
The derived and implemented multivariate likelihood function directly incorporates diffraction data collected from a SAD experiment and models the correlations and errors that occur in the experiment and process. As a result, the SAD likelihood function can refine and improve model and heavy-atom parameters together, allowing direct and dynamic incorporation of the experimental phase information. The simultaneous of the available parameters combined with a multivariate analysis in the SAD likelihood function appeared to result in a synergic effect that enabled ARP/wARP and REFMAC5 to build the subtilisin molecule successfully when current likelihood targets failed. From the thioesterase test case, it appears that if the starting experimental phase information is of sufficient quality, the existing likelihood function incorporating prior phase information can be used to construct automatically a model of similar quality to the SAD function.
The above results are promising, but further test cases will be performed to determine whether the trend continues. In particular, test cases with diffraction data at lower resolution will be performed to determine whether the additional information provided by the direct and dynamic incorporation of experimental phase information will push the resolution limits needed for automated building techniques.
In the future, likelihood-based gradient difference maps (e.g. de La Fortelle & Bricogne, 1997![La Fortelle, E. de & Bricogne, G. (1997). Methods Enzymol. 276, 472-494. [La Fortelle, E. de & Bricogne, G. (1997). Methods Enzymol. 276, 472-494.]](../../../../../../logos/arrows/d_arr.gif) ) will be considered in order to identify any previously undetected anomalous sites. In addition, a multivariate likelihood function will be implemented that incorporates the experimental diffraction data from any variety of phasing experiments [i.e. S/MIR(AS) and/or MAD].
) will be considered in order to identify any previously undetected anomalous sites. In addition, a multivariate likelihood function will be implemented that incorporates the experimental diffraction data from any variety of phasing experiments [i.e. S/MIR(AS) and/or MAD].
The distribution derived above can also be used for the of structure and structure–ligand complexes that directly model the correlation between the observations and the models. Combining the diffraction information from a native structure and a structure in a complex may help emphasize the differences between them, which is usually of major interest to structural biologists, and considering all available information directly may lead to more efficient structure determinations.
APPENDIX A
A1. Derivation of the required distribution
The conditional probability distribution of two observed structure-factor amplitudes, given M model structure factors, will be derived. The SAD likelihood function is the special case when M = 2.
The starting point for the derivation will be the multivariate complex Gaussian probability distribution of structure factors (Pannu et al., 2003). Below, N structure factors will be considered, F1, F2, F3, …, FN, where F1 and F2 represent the `observed' structure factors and N = M + 2. The amplitude of a Fi will be denoted |Fi| and its phase αi.
In the above expression, ΣN is the Hermitian covariance matrix of this N-dimensional probability distribution and zij denotes the ijth element of the inverse matrix of ΣN. The equation can be rewritten by separately summing over the diagonal and off-diagonal terms,
After transforming to polar coordinates and simplifying, we obtain
In the above equation, aij and bij represent the real and imaginary components of the inverse covariance matrix. The unknown phase angles α1 and α2 are now integrated out.
The inner integral can be solved analytically,
I0(x) is the modified Bessel function of zeroth order. The marginal distribution can now be written as a function involving only one integral,
where
Using the definition of conditional probability, the required probability distribution can be obtained as
P(|F1|, |F2|, |F3|, α3, …, |FN|, αN) is given in (8)![[link]](../../../../../../logos/arrows/d_arr.gif) and P(|F3|, α3, …, |FN|, αN) can be obtained from (5)
and P(|F3|, α3, …, |FN|, αN) can be obtained from (5)![[link]](../../../../../../logos/arrows/d_arr.gif) , denoting the corresponding covariance matrix by ΣN−2 and the ijth element of its inverse by cij + idij. Thus, the required distribution can be expressed as
, denoting the corresponding covariance matrix by ΣN−2 and the ijth element of its inverse by cij + idij. Thus, the required distribution can be expressed as
Acknowledgements
The authors thank S. R. Ness for advice on the use of the automated structure-solution system CRANK, A. Perrakis, R. A. G. de Graaff and J. P. Abrahams for useful discussions and Z. Dauter and colleagues for providing the diffraction data used in the test cases. Funding for this work was provided by Leiden University and the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO). GNM thanks the Wellcome Trust for support.
References
 Anderson, E., Bai, Z., Bischof, C., Blackford, S., Demmel, J., Dongarra, J., Du Croz, J., Greenbaum, A., Hammarling, S., McKenney, A. & Sorensen, D. (1999). LAPACK Users' Guide, 3rd ed. Philadelphia: Society for Industrial and Applied Mathematics. Google Scholar
Anderson, E., Bai, Z., Bischof, C., Blackford, S., Demmel, J., Dongarra, J., Du Croz, J., Greenbaum, A., Hammarling, S., McKenney, A. & Sorensen, D. (1999). LAPACK Users' Guide, 3rd ed. Philadelphia: Society for Industrial and Applied Mathematics. Google Scholar
 Bricogne, G. (2000). Advanced Special Functions and Applications: Proceedings of the Melfi School on Advanced Topics in Mathematics and Physics, edited by D. Cocolicchio, G. Dattoli & H. M. Srivastava, pp. 315–323. Rome: Aracne Editrice. Google Scholar
Bricogne, G. (2000). Advanced Special Functions and Applications: Proceedings of the Melfi School on Advanced Topics in Mathematics and Physics, edited by D. Cocolicchio, G. Dattoli & H. M. Srivastava, pp. 315–323. Rome: Aracne Editrice. Google Scholar
 Bricogne, G. & Irwin, J. (1996). Proceedings of the CCP4 Study Weekend. Macromolecular Refinement, edited by E. J. Dodson, M. Moore, A. Ralph & S. Bailey, pp. 85–92. Warrington: Daresbury Laboratory. Google Scholar
Bricogne, G. & Irwin, J. (1996). Proceedings of the CCP4 Study Weekend. Macromolecular Refinement, edited by E. J. Dodson, M. Moore, A. Ralph & S. Bailey, pp. 85–92. Warrington: Daresbury Laboratory. Google Scholar
 Burla, M. C., Carrozzini, B., Cascarano, G. L., Giacovazzo, C., Polidori, G. & Siliqi, G. (2002). Acta Cryst. D58, 928–935. Web of Science CrossRef CAS IUCr Journals Google Scholar
Burla, M. C., Carrozzini, B., Cascarano, G. L., Giacovazzo, C., Polidori, G. & Siliqi, G. (2002). Acta Cryst. D58, 928–935. Web of Science CrossRef CAS IUCr Journals Google Scholar
 Collaborative Computational Project, Number 4 (1994). Acta Cryst. D50, 760–763. CrossRef IUCr Journals Google Scholar
Collaborative Computational Project, Number 4 (1994). Acta Cryst. D50, 760–763. CrossRef IUCr Journals Google Scholar
 Cowtan, K. (1994). Jnt CCP4/ESF–EAMCB Newsl. Protein Crystallogr. 31, 34–38. Google Scholar
Cowtan, K. (1994). Jnt CCP4/ESF–EAMCB Newsl. Protein Crystallogr. 31, 34–38. Google Scholar
 Dauter, Z., Dauter, M. & Dodson, E. J. (2002). Acta Cryst. D58, 494–506. Web of Science CrossRef CAS IUCr Journals Google Scholar
Dauter, Z., Dauter, M. & Dodson, E. J. (2002). Acta Cryst. D58, 494–506. Web of Science CrossRef CAS IUCr Journals Google Scholar
 Giacovazzo, C. & Siliqi, G. (2001a). Acta Cryst. A57, 40–46. Web of Science CrossRef CAS IUCr Journals Google Scholar
Giacovazzo, C. & Siliqi, G. (2001a). Acta Cryst. A57, 40–46. Web of Science CrossRef CAS IUCr Journals Google Scholar
 Giacovazzo, C. & Siliqi, G. (2001b). Acta Cryst. A57, 414–419. Web of Science CrossRef CAS IUCr Journals Google Scholar
Giacovazzo, C. & Siliqi, G. (2001b). Acta Cryst. A57, 414–419. Web of Science CrossRef CAS IUCr Journals Google Scholar
 Giacovazzo, C. & Siliqi, G. (2004). Acta Cryst. D60, 73–82. Web of Science CrossRef CAS IUCr Journals Google Scholar
Giacovazzo, C. & Siliqi, G. (2004). Acta Cryst. D60, 73–82. Web of Science CrossRef CAS IUCr Journals Google Scholar
 Graaff, R. A. G. de, Hilge, M., van der Plas, J. L. & Abrahams, J. P. (2001). Acta Cryst. D57, 1857–1862. Web of Science CrossRef IUCr Journals Google Scholar
Graaff, R. A. G. de, Hilge, M., van der Plas, J. L. & Abrahams, J. P. (2001). Acta Cryst. D57, 1857–1862. Web of Science CrossRef IUCr Journals Google Scholar
 Hendrickson, W. A. & Lattman, E. E. (1970). Acta Cryst. B26, 136–143. CrossRef CAS IUCr Journals Google Scholar
Hendrickson, W. A. & Lattman, E. E. (1970). Acta Cryst. B26, 136–143. CrossRef CAS IUCr Journals Google Scholar
 La Fortelle, E. de & Bricogne, G. (1997). Methods Enzymol. 276, 472–494. Google Scholar
La Fortelle, E. de & Bricogne, G. (1997). Methods Enzymol. 276, 472–494. Google Scholar
 Li, J., Derewenda, U., Dauter, Z., Smith, S. & Derewenda, Z. S. (2000). Nature Struct. Biol. 7, 555–559. CrossRef PubMed CAS Google Scholar
Li, J., Derewenda, U., Dauter, Z., Smith, S. & Derewenda, Z. S. (2000). Nature Struct. Biol. 7, 555–559. CrossRef PubMed CAS Google Scholar
 Murshudov, G. N., Vagin, A. A. & Dodson, E. J. (1997). Acta Cryst. D53, 240–255. CrossRef CAS Web of Science IUCr Journals Google Scholar
Murshudov, G. N., Vagin, A. A. & Dodson, E. J. (1997). Acta Cryst. D53, 240–255. CrossRef CAS Web of Science IUCr Journals Google Scholar
 Ness, S. R., de Graaff, R. A. G., Abrahams, J. P. & Pannu, N. S. (2004). Structure, 12, 1753–1761. Web of Science CrossRef PubMed CAS Google Scholar
Ness, S. R., de Graaff, R. A. G., Abrahams, J. P. & Pannu, N. S. (2004). Structure, 12, 1753–1761. Web of Science CrossRef PubMed CAS Google Scholar
 Pannu, N. S., McCoy, A. J. & Read, R. J. (2003). Acta Cryst. D59, 1801–1808. Web of Science CrossRef CAS IUCr Journals Google Scholar
Pannu, N. S., McCoy, A. J. & Read, R. J. (2003). Acta Cryst. D59, 1801–1808. Web of Science CrossRef CAS IUCr Journals Google Scholar
 Pannu, N. S., Murshudov, G. N., Dodson, E. J. & Read, R. J. (1998). Acta Cryst. D54, 1285–1294. Web of Science CrossRef CAS IUCr Journals Google Scholar
Pannu, N. S., Murshudov, G. N., Dodson, E. J. & Read, R. J. (1998). Acta Cryst. D54, 1285–1294. Web of Science CrossRef CAS IUCr Journals Google Scholar
 Pannu, N. S. & Read, R. J. (1996). Acta Cryst. A52, 659–668. CrossRef CAS Web of Science IUCr Journals Google Scholar
Pannu, N. S. & Read, R. J. (1996). Acta Cryst. A52, 659–668. CrossRef CAS Web of Science IUCr Journals Google Scholar
 Pannu, N. S. & Read, R. J. (2004). Acta Cryst. D60, 22–27. Web of Science CrossRef CAS IUCr Journals Google Scholar
Pannu, N. S. & Read, R. J. (2004). Acta Cryst. D60, 22–27. Web of Science CrossRef CAS IUCr Journals Google Scholar
 Perrakis, A., Morris, R. & Lamzin, V. S. (1999). Nature Struct. Biol. 6, 458–463. Web of Science CrossRef PubMed CAS Google Scholar
Perrakis, A., Morris, R. & Lamzin, V. S. (1999). Nature Struct. Biol. 6, 458–463. Web of Science CrossRef PubMed CAS Google Scholar
 Rice, L. M. & Brünger, A. T. (1994). Proteins, 19, 277–290. CrossRef CAS PubMed Web of Science Google Scholar
Rice, L. M. & Brünger, A. T. (1994). Proteins, 19, 277–290. CrossRef CAS PubMed Web of Science Google Scholar
 Scheres, S. H. W. & Gros, P. (2001). Acta Cryst. D57, 1820–1828. Web of Science CrossRef CAS IUCr Journals Google Scholar
Scheres, S. H. W. & Gros, P. (2001). Acta Cryst. D57, 1820–1828. Web of Science CrossRef CAS IUCr Journals Google Scholar
 Terwilliger, T. C. (2003). Acta Cryst. D59, 1174–1182. Web of Science CrossRef CAS IUCr Journals Google Scholar
Terwilliger, T. C. (2003). Acta Cryst. D59, 1174–1182. Web of Science CrossRef CAS IUCr Journals Google Scholar
© International Union of Crystallography. Prior permission is not required to reproduce short quotations, tables and figures from this article, provided the original authors and source are cited. For more information, click here.


 journal menu
journal menu
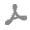





![[\eqalignno{ P_{\rm SAD} & = P(|F^+|, |F^-|\semi |F_c^+|, \alpha_c^+, |F_c^-|, \alpha_c^-) \cr &= {{ 2 |F^+| |F^-| \det(\Sigma_2)} \over {\pi \det(\Sigma_4)}} \cr &\ \quad {\times}\ \exp [ - a_{11} |F^+|^2 - a_{22} |F^-|^2 - (a_{33} - c_{33}) |F_c^+|^2] \cr &\ \quad {\times}\ \exp\{ - (a_{44} - c_{44}) |F_c^-|^2 - 2 |F_c^+| |F_c^-| \cr &\ \quad {\times}\ [ (a_{34} - c_{34}) \cos(\alpha_3 - \alpha_4) - (b_{34} - d_{34}) \sin(\alpha_3 - \alpha_4)]\} \cr &\ \quad {\times} \textstyle \int\limits_0^{2\pi} \big( \exp\{- 2|F^-| |F_c^+|[ a_{23} \cos(\alpha^- - \alpha_c^+) \cr &\ \quad -\ b_{23} \sin(\alpha^- - \alpha_c^+)]\} \exp\{- 2|F^-| |F_c^-| \cr &\ \quad {\times}\ [a_{24} \cos(\alpha^- - \alpha_c^-) - b_{24} \sin(\alpha^- - \alpha_c^-)]\} \cr &\ \quad {\times}\ {I_0}[{\xi (|F^+|, |F^-|, |F_c^+|, \alpha_c^+, |F_c^-|, \alpha_c^-, \Sigma_4^{-1})}]^{1/2}\big) \,\, {\rm d} \alpha^-, \cr && (1)} ]](teximages/ba5062fd1.gif)
![[\eqalignno{ \xi (|F^+|, |F^-|, &\alpha^-, |F_c^+|, \alpha_c^+, |F_c^-|, \alpha_c^-, \Sigma_4^{-1}) \cr & = 4 |F^+|^2 \{[a_{12} |F^-| \cos(\alpha^-) + b_{12} |F^-| \sin(\alpha^-) \cr &\ \quad +\ a_{13} |F_c^+| \cos(\alpha_c^+) + b_{13} |F_c^+| \sin(\alpha_c^+) \cr &\ \quad +\ a_{14} |F_c^-| \cos(\alpha_c^-) + b_{14} |F_c^-| \sin(\alpha_c^-)]^2 \cr &\ \quad +\ [ a_{12} |F^-| \sin(\alpha^-) - b_{12} |F^-| \cos(\alpha^-) \cr &\ \quad +\ a_{13} |F_c^+| \sin(\alpha_c^+) - b_{13} |F_c^+| \cos(\alpha_c^+) \cr &\ \quad +\ a_{14} |F_c^-| \sin(\alpha_c^-) - b_{14} |F_c^-| \cos(\alpha_c^-)]^2\}. & (2)}]](teximages/ba5062fd2.gif)
![[P (F_1, F_2, \ldots, F_{N}) = {{1}\over{\pi^N\det(\Sigma_{N})}} \exp \left(-{\textstyle\sum\limits_{i = 1}^N \sum\limits_{j = 1}^N} F^*_i z_{ij} F_j \right). \eqno(3)]](teximages/ba5062fd3.gif)
![[\eqalignno{ P (F_1, F_2, \ldots, F_{N}) & = {{1}\over{\pi^N\det(\Sigma_{N})}}&(4) \cr &\quad \times \exp \left\{-{\textstyle\sum\limits_{i = 1}^N} \left[|F_i|^2 z_{ii} + {\textstyle \sum\limits_{j = i+1}^N} 2\Re \left(F^*_i F_j z_{ij} \right) \right] \right \}. }]](teximages/ba5062fd4.gif)
![[\eqalignno{ P (|F_1|, &\alpha_1, |F_2|,\alpha_2, \ldots, |F_{N}|, \alpha_N)& (5) \cr &= {{\textstyle \prod_{i = 1}^N |F_i|}\over{\pi^N\det(\Sigma_{N})}} \exp \biggr[-\textstyle\sum\limits_{i = 1}^N \biggr(|F_i|^2 a_{ii} \cr & \quad + \textstyle\sum\limits_{j = i+1}^N \{2 |F_i| |F_j| \big[a_{ij} \cos(\alpha_j-\alpha_i) - b_{ij} \sin(\alpha_j-\alpha_i) ]\} \biggr) \biggr]. }]](teximages/ba5062fd5.gif)
![[\eqalignno{ P &(|F_1|, |F_2|, |F_3|,\alpha_3, \ldots, |F_{N}|, \alpha_N) \cr & = {{\prod_{i = 1}^N |F_i|}\over{\pi^N\det(\Sigma_{N})}} \exp \biggr[- |F_1|^2 a_{11} - |F_2|^2 a_{22} -\textstyle\sum\limits_{i = 3}^N \biggr(|F_i|^2 a_{ii} \cr & \quad + \textstyle\sum\limits_{j = i+1}^N \{ 2 |F_i| |F_j| [ a_{ij} \cos(\alpha_j-\alpha_i) - b_{ij} \sin(\alpha_j-\alpha_i) ]\} \biggr ) \biggr] \cr & \quad\times {\textstyle \int\limits_0^{2\pi}} \exp \biggr(-\textstyle\sum\limits_{i = 2}^N \{2 |F_2| |F_i| \cr & \quad \times[ a_{2i} \cos(\alpha_i-\alpha_2) - b_{2i} \sin(\alpha_i-\alpha_2) ] \} \biggr) \cr & \quad \times {\textstyle \int\limits_0^{2\pi}} \exp \biggr(-\textstyle\sum\limits_{i = 2}^N \{2 |F_1| |F_i| \cr & \quad\times[a_{1i} \cos(\alpha_i-\alpha_1) - b_{1i} \sin(\alpha_i-\alpha_1) ]\} \biggr) \, {\rm d} \alpha_1 \,\, {\rm d}\alpha_2. & (6)}]](teximages/ba5062fd6.gif)
![[\eqalignno{ {\textstyle \int\limits_0^{2\pi}}\exp & \biggr(-\textstyle\sum\limits_{i = 2}^N \{2 |F_1| |F_i| \cr &\ \quad {\times}\ [a_{1i} \cos(\alpha_i-\alpha_1) - b_{1i} \sin(\alpha_i-\alpha_1) ] \} \biggr) \, {\rm d}\alpha_1 \cr & = {\textstyle \int\limits_0^{2\pi}}\exp \biggr\{- 2 \cos \alpha_1 |F_1| \textstyle\sum\limits_{i = 2}^N [ |F_i| (a_{1i} \cos \alpha_i - b_{1i} \sin \alpha_i )] \cr & \quad -2 \sin \alpha_1 |F_1| \textstyle\sum\limits_{i = 2}^N [|F_i| (a_{1i} \sin \alpha_i + b_{1i} \cos \alpha_i ) ] \biggr\} \, {\rm d}\alpha_1 \cr & = 2 \pi I_0 \biggr( 4|F_1|^2 \biggr\{\biggr[\textstyle\sum\limits_{i = 2}^N |F_i| (a_{1i} \cos \alpha_i - b_{1i} \sin \alpha_i) \biggr] ^2 \cr & \quad+ \biggr[\sum_{i = 2}^N |F_i| (a_{1i} \sin \alpha_i + b_{1i} \cos \alpha_i) \biggr] ^2 \biggr\} \biggr)^{1/2}. & (7)}]](teximages/ba5062fd7.gif)
![[\eqalignno{ P (|F_1|,& |F_2|, |F_3|,\alpha_3, \ldots, |F_{N}|, \alpha_N) = 2{{\prod_{i = 1}^N |F_i|}\over{\pi^{N-1}\det(\Sigma_{N})}} \cr & \times \exp \biggr[- |F_1|^2 a_{11} - |F_2|^2 a_{22} -\textstyle\sum\limits_{i = 3}^N \biggr(|F_i|^2 a_{ii} \cr & + \textstyle\sum\limits_{j = i+1}^N \biggr\{ 2 |F_i| |F_j| [ a_{ij} \cos(\alpha_j-\alpha_i) - b_{ij} \sin(\alpha_j-\alpha_i) ] \biggr\} \biggr) \biggr] \cr & \times I_0 (2|F_1| \xi){\textstyle \int\limits_0^{2\pi}}\exp \biggr(-\textstyle\sum\limits_{i = 2}^N \{2 |F_2| |F_i| \cr & \times[a_{2i} \cos(\alpha_i-\alpha_2) - b_{2i} \sin(\alpha_i-\alpha_2) ] \} \biggr) \, {\rm d}\alpha_2, & (8)}]](teximages/ba5062fd8.gif)
![[\eqalignno{ \xi = & \, \biggr( \textstyle\sum\limits_{i = 2}^N \biggr\{ |F_i|^2 (a_{1i}^2 + b_{1i}^2) + \sum\limits_{j = i+1}^N 2|F_i||F_j| [ (a_{1i}a_{1j}+b_{1i}b_{1j}) \cr & \times \cos (\alpha_j-\alpha_i) + (a_{1j}b_{1i}-a_{1i}b_{1j}) \sin (\alpha_j-\alpha_i) ] \biggr\} \biggr)^{1/2}. & (9)}]](teximages/ba5062fd9.gif)
![[\eqalignno{ P (|F_1|, |F_2| \semi & |F_3|, \alpha_3, \ldots, |F_{N}|, \alpha_N) \cr & = \, {{ P (|F_1|, |F_2|, |F_3|, \alpha_3, \ldots, |F_{N}|, \alpha_N) } \over { P (|F_3|, \alpha_3, \ldots, |F_{N}|, \alpha_N) }}. & (10)}]](teximages/ba5062fd10.gif)
![[\eqalignno{ P (|&F_1|, |F_2|\semi |F_3|, \alpha_3, \ldots, |F_{N}|, \alpha_N) = {{ 2|F_1||F_2| \det(\Sigma_{N-2}) }\over {\pi \det(\Sigma_{N})}} \cr & \times\exp \biggr[- |F_1|^2 a_{11} - |F_2|^2 a_{22} -\textstyle\sum\limits_{i = 3}^N \biggr(|F_i|^2 (a_{ii}-c_{ii}) \cr & + \textstyle\sum\limits_{j = i+1}^N \{ 2 |F_i| |F_j| [ (a_{ij}-c_{ij}) \cos(\alpha_j-\alpha_i) \cr & - (b_{ij}-d_{ij}) \sin(\alpha_j-\alpha_i) ] \} \biggr) \biggr] {\textstyle \int\limits_0^{2\pi}} \exp \biggr(-\textstyle\sum\limits_{i = 2}^N \{ 2 |F_2| |F_i| \cr & \times[ a_{2i} \cos(\alpha_i-\alpha_2) - b_{2i} \sin(\alpha_i-\alpha_2)]\} \biggr) I_0 (2|F_1| \xi) \,\, {\rm d} \alpha_2. & (11)}]](teximages/ba5062fd11.gif)